NUMERICAL ANALYSIS AND SCIENTIFIC COMPUTING
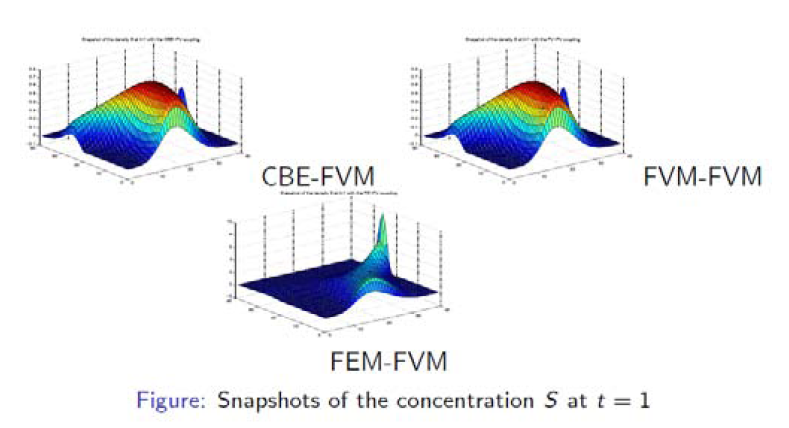
Multiscale Modeling and ComputationMultiscale modeling and computation is a rapidly evolving area of research in computational science and engineering such as material science, chemistry, fluid dynamics and biology. For example, natural porous media have extreme heterogeneity which requires multiscale modeling and computation. Moreover, most of the differential equations encountered in physics embody some sort of conservation law. It is therefore important to try to ensure that the method chosen to solve the equation obeys the underlying conservation law exactly. We introduced a new class of locally conservative methods and analyzed for second-order elliptic equations. As in the discontinuous Galerkin finite element method, we try to combine the finite element and finite volume methods by incorporating the governing equation in a sense closer to the finite volume method.
Modeling and Optimal Control of infectious disease
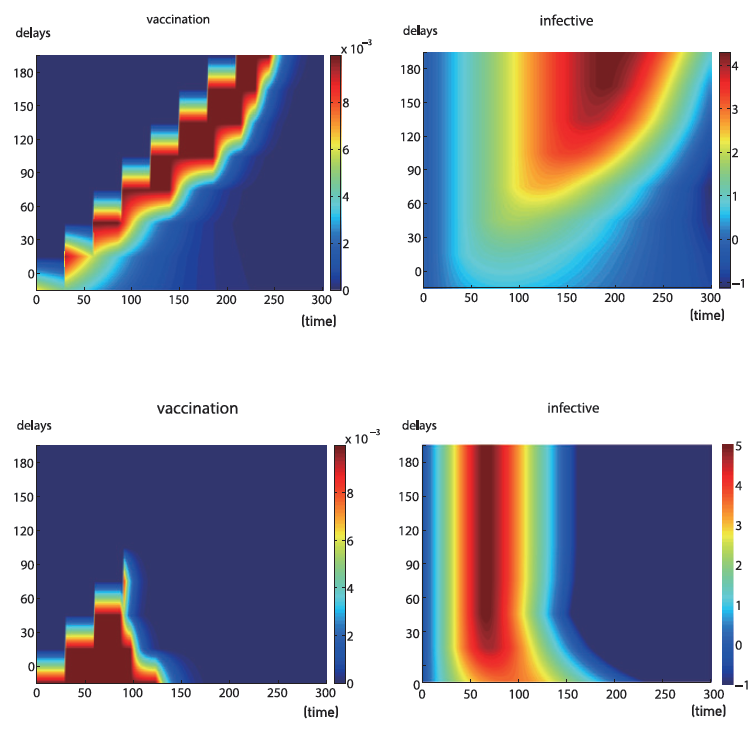
Our model for influenza is based on the standard SLIAR, a deterministic compartmental model, where S, L, I, A, and R denote the numbers of individuals in the susceptible, latent, infective, asymptomatic, and recovered compartments, respectively. Parameter values used in the model include initial population of each compartment, fatal rate, latent period, ratio of asymptomatic, basic reproduction number, contact rate, and contagiousness. We added controls of vaccination, antiviral treatment and isolation and related parameters such as effect and cost of those control measures to compare and/or evaluate various control strategies. Then we applied optimization theory to find optimal control in each setting of objective functional. We performed numerical simulations with various set of parameters to investigate the effect of control measures. We also observed the change of optimal strategies according to the change in parameters and objective. 30% was vaccinated during 100-130 days after the initial time and infective individuals reduce their contact rate by 20%. Optimal control depends on the choice of mathematical models, estimation of parameters, objective controls. For example, when the costs of controls are different, the optimal strategy tends to reduce the use of an expensive treatment. Effective strategy also changes corresponding to parameter values including fatal rate, latent period, ratio of asymptomatic, basic reproduction number, contact rate, and contagiousness, which represent the disease characteristics. While the details of optimal strategy changes according to each setting, some qualitative advice suggested by the various runs is consistent, e.g. early vaccination, if available, is an essential tool in fighting an epidemic.
Green's function for parabolic systems with Neumann condition
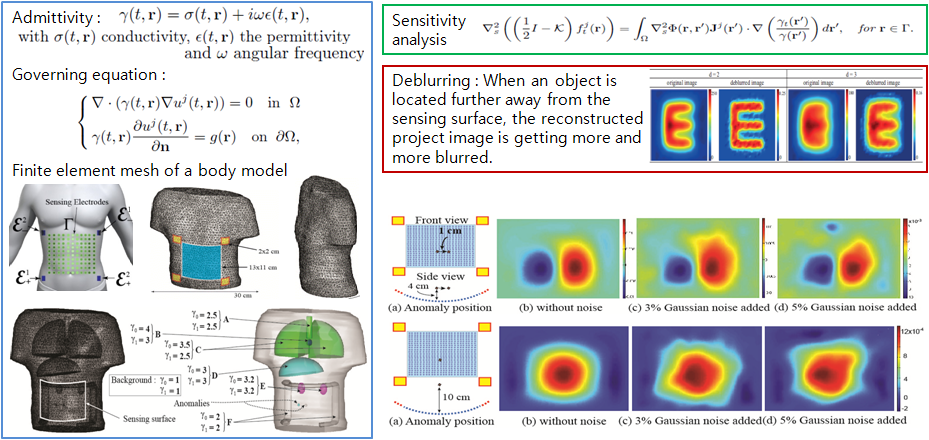
Lung Monitoring in EIT using Finite Element Method
Admitting fundamental limitations of EIT methods in providing high resolution image for the interior region away from the boundary, it would be desirable to pay attention to high resolution impedance image in a near-surface region. Lately, we propose a new EIT system that has a unique electrode configuration and associated data collection method. In this new system, two pairs of driving electrodes are attached on the four sides of the surface of the body, and an array of many voltage-sensing electrodes is attached on the surface as shown in figure below. The advantage of the separation of current injection and voltage sensing electrodes is that no current flows through the contact impedance of a voltage sensing electrode and therefore the contact impedance contributions on measured voltage values are negligible. When we inject current using a pair of driving electrodes, the induced internal current will flow underneath the voltage sensing electrodes, and we can measure voltages between equipotential lines in the normal direction to the voltage sensing electrode array.
|
A finite element eddy-viscosity method for turbulence modelIt is generally accepted that incompressible fluid flows, even for high values of the Reynolds number are faithfully modeled by the Navier-Stokes system. The direct computational simulation of the Navier-Stokes system in turbulent regimes is a formidable task due to the disparate scales that have to be resolved. Turbulence modeling attempts to mitigate this situation by somehow accounting for the effects of small-scale behavior on those at large-scales without explicitly resolving the small scales. One such approach is to add viscosity to the problem; the Smagorinsky and Ladyzhenskaya models and other eddy-viscosity models are examples of this approach. In 1969 and 1970, Ladyzhenskaya proposed a turbulent model and the Smagorinsky model corresponds to the special case. Unfortunately, these approach usually results in over-dampening at the large scales, i.e., large-scale structures are unphysically smeared out. To mitigate this fault of eddy-viscosity modeling, filtered eddy-viscosity methods that add the artificial viscosity only to the high-frequency modes were developed in the context of spectral methods by using the damping operator Q, which is called a high-pass filter. This research applies the filtered eddy-viscosity idea to finite element methods with hierarchical basis functions and the existence and uniqueness of the finite element approximation has been proved. Its convergence to a weak solution of the Navier-Stokes system also has been analyzed.
Superconvergent discontinuous Galerkin methods
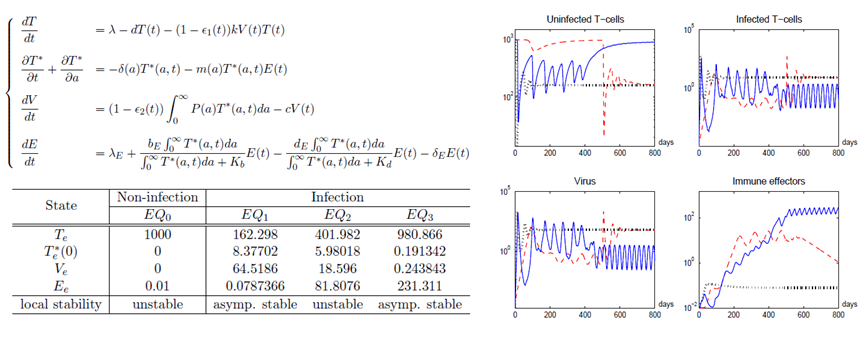
Optimal therapy protocols for HIV infection
We developed an age-structured model of HIV infection with various compartments, including target cells, infected cells, viral loads and immune effector cells, to provide a better understanding of the interaction between HIV and the immune system. We show that the proposed model has one uninfected steady state and several infected steady states. We conduct a local stability analysis of these steady. In addition, we study various techniques and ideas from optimal control theory to derive optimal therapy protocols. The results of numerical simulations indicate that the optimal therapy protocols can facilitate long-term control of HIV through a strong immune response after the discontinuation of the therapy.
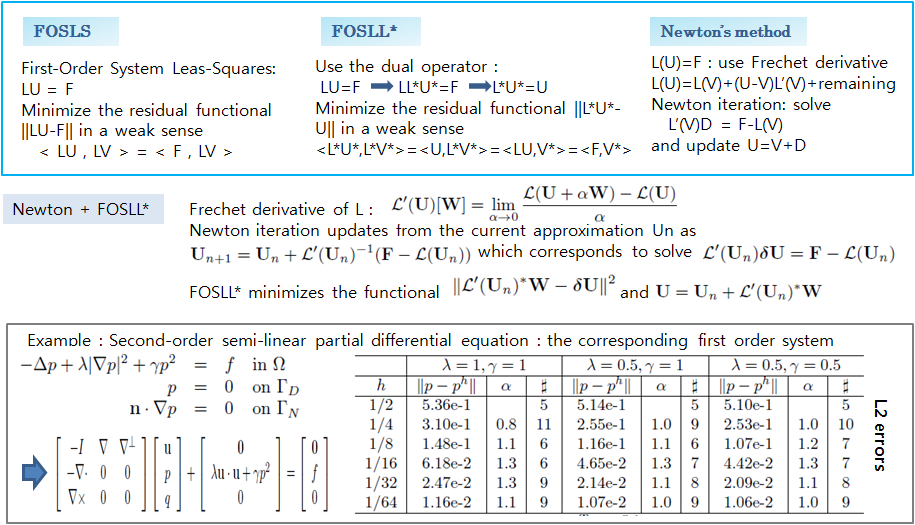
FOSLL* Approach for Nonlinear Partial Differential Equations
The first-order system LL*(FOSLL*) method was first used in Newton-FOSLS iterations to improve mass conservation of Navier-Stokes problem. It is known that the least-squares finite element method typically provides poor conservation in fluid motion because it minimizes the continuity equation in L2-norm instead of using exact discrete mass conservative form. However, by using FOSLL* with a modification of normal vectors in Newton iteration instead of FOSLS at the last iterate, mass loss was greatly improved. While getting improved mass conservation by using FOSLL* only at the last stage of Newton iterations, questions arose what happens if FOSLL* was used in several stages in Newton iterations and how this process can be generalized. The difficulties in applying FOSLL* in Newton iterations and the generalization are being studied currently.
Nonlinear Mixed FEM and AdaptivityThe mixed finite element method has two important features. It conserves the mass locally and produces accurate flux even for highly non-homogeneous media with large jumps in the physical properties. Compared with existing literature, several improvements are made in this work on mixed methods for nonlinear elliptic problems. First, the Raviart-Thomas-Nedelec finite element space of all orders including the lowest order case are treated. Existence and uniqueness of the approximate solution to the model problem is proved.
|